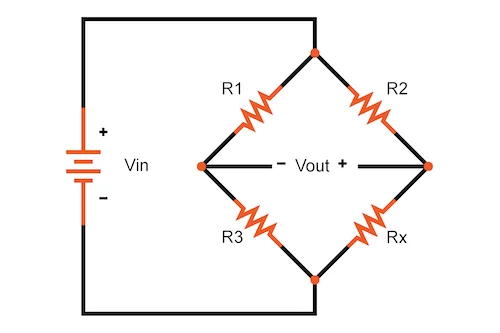
Принцип измерения сопротивления основан на уравнивании потенциала средних выводов двух ветвей моста из четырёх резисторов. Используя в качестве измеряемого сопротивления терморезистор, зная его температурный коэффициент можно точно вычислять изменения температуры.

Преимуществом мостовой схемы является возможность компенсации синфазных помех и дрейфа напряжения питания.

Теоретические основы и формула баланса

Мостовая схема состоит из четырех резистивных плеч, образующих замкнутый контур. На одну диагональ подается напряжение питания V_in, а с другой снимается дифференциальный сигнал V_out. В одну из ветвей включён резистор, сопротивление которого требуется измерить - R_x.

Для лучшей повторяемости и точности нужно подбирать номиналы как Это даст максимум чувствительности и 0 Вольт в начале шкалы.

R_x - в описываемой схеме это терморезистор (в примере ниже взят Pt1000), а сопротивления остальных резисторов равны его сопротивлению при температуре 0°С.


Состояние баланса, при котором V_out = 0, достигается при условии равенства отношений сопротивлений плеч:

R₃ / R₁ = R_x / R₂

При повышении температуры сопротивление R_x изменяется, таким образом появляется разность потенциалов между точками соединения R₁R₃ и R₂R_x.

Выходное напряжение V_out в такой схеме будет рассчитываться по следующей формуле:

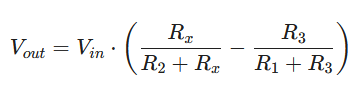
Общая формула температурного коэффициента

Для любого терморезистора (как с положительным, так и с отрицательным температурным коэффициентом) фундаментальное значение имеет зависимость его сопротивления от температуры. Общая формула для линейного приближения в ограниченном диапазоне температур выглядит следующим образом:

R = R₀ (1 + α (T - T₀))

Где:

• R - сопротивление при температуре T (оно же искомое R_x)
• R₀ - номинальное сопротивление при референсной температуре T₀ (обычно 0°C или 25°C)
• α - температурный коэффициент сопротивления, °C^-1

В прецизионных приложениях, где требуется учет нелинейности, используется уравнение Каллендара-Ван Дюзена, добавляющее квадратичные и кубические члены, однако для большинства промышленных задач линейной аппроксимации достаточно.

Итоговые формулы расчёта температуры

Полные формулы расчёта температуры можно при необходимости вывести из формулы выходного напряжение, здесь же приведём лишь итоговые формулы для случая, когда все резисторы моста выбраны одного номинала R_ном.

Для платиновых датчиков (RTD, например Pt100 или Pt1000) используется линейная аппроксимация (для диапазона 0...100°C):

Для NTC-термисторов: Используется уравнение Стейнхарта-Харта (упрощенное через B-коэффициент): Здесь T₀​ — температура калибровки в Кельвинах (для 25°C это 298.15),
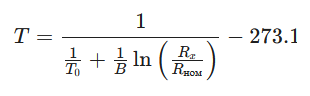
B — параметр из даташита вашего термистора (обычно в пределах 3000–4500).

Аспекты практической реализации

Есть две основных ошибки, встречающиеся в практической реализации — это игнорирование допуска номиналов резисторов, а также пренебрежение входным сопротивлением измерительного каскада. Теоретическая формула предполагает, что ток через выходную диагональ не течет, однако в реальности любой вольтметр или АЦП имеет конечное сопротивление.
Если к выходу моста подключен усилитель с низким входным сопротивлением R_load​, он начинает шунтировать плечи моста, что искажает результаты. Это особенно критично при использовании микроконтроллеров со встроенными АЦП, входное сопротивление которых может варьироваться в процессе дискретизации. Для исключения этой ошибки схему обычно подключают через буферный каскад на операционном усилителе с высоким входным импедансом.

Пример расчета для Pt1000

Рассмотрим использование платинового терморезистора Pt1000 в качестве измерительного элемента. Данный тип датчика обладает номинальным сопротивлением 1000 Ом при 0°C и стандартным коэффициентом α = 0.00385 °C^-1 согласно IEC 60751.

Предположим, что датчик интегрирован в мостовую схему для контроля перегрева шунта в системе распределения питания. Если при протекании тока температура датчика за счет теплового контакта увеличилась до 50°C, его расчетное сопротивление составит:

R = 1000 · (1 + 0.00385 (50 - 0)) = 1192.5 Ом

Выбор именно Pt1000 вместо более распространённого Pt100 обусловлен рядом преимуществ: более высокое сопротивление позволяет значительно снизить ток возбуждения (обычно до 0.1–0.5 мА), что минимизирует ошибку от собственного нагрева датчика и делает его идеальным для батарейного питания.

Температура, °C	Сопротивление, Ом	Допуск (Класс A), ±°С
-20	921.6	0.19
0	1000.0	0.15
20	1077.9	0.19
50	1194.0	0.25
100	1385.1	0.35